In previous Windows versions like Windows XP, it was possible to change the system font used in menus, Explorer, on Desktop and so on. There was an easy to use option in the GUI which allowed you to change the system font with one click. However, in Windows 10 there is no such option. The operating system lacks this ability. Here is a trick which will allow you to bypass this limitation.
Advertisеment
By default, Windows 10 is using the font named Segoe UI everywhere in Desktop components. It is used for context menus, for Explorer icons and so on. With a simple Registry tweak, you can change it.
Tip: you can save your time and use Winaero Tweaker instead of Registry editing! The following user interface will allow you to change system font in Windows 10:
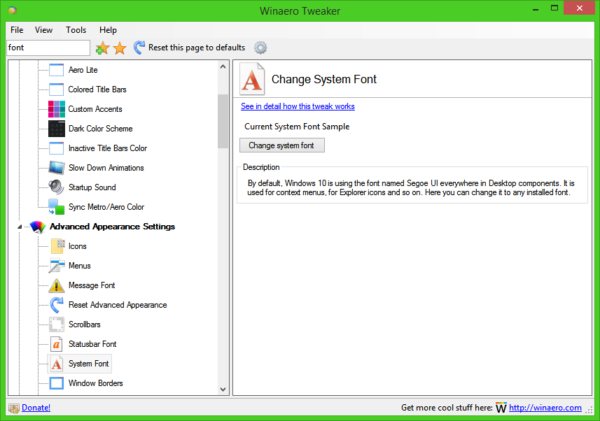 Get Winaero Tweaker here: Download Winaero Tweaker.
Get Winaero Tweaker here: Download Winaero Tweaker.
To change system font in Windows 10, do the following.
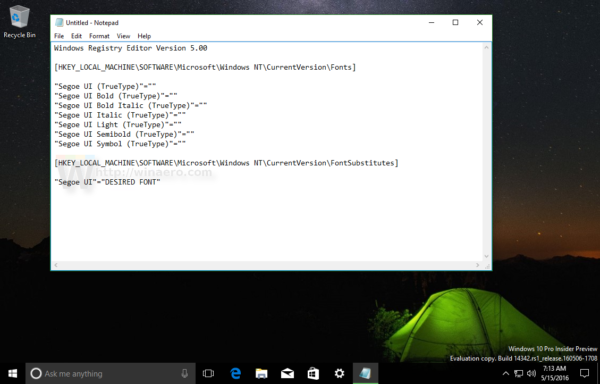
Open Notepad, then copy and paste the following text:
Windows Registry Editor Version 5.00 [HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows NT\CurrentVersion\Fonts] "Segoe UI (TrueType)"="" "Segoe UI Bold (TrueType)"="" "Segoe UI Bold Italic (TrueType)"="" "Segoe UI Italic (TrueType)"="" "Segoe UI Light (TrueType)"="" "Segoe UI Semibold (TrueType)"="" "Segoe UI Symbol (TrueType)"="" [HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows NT\CurrentVersion\FontSubstitutes] "Segoe UI"="DESIRED FONT"
 Replace the DESIRED FONT portion with the desired font name. It can be Times New Roman, Tahoma, or Comic Sans etc - any font you have installed in Windows 10.
Replace the DESIRED FONT portion with the desired font name. It can be Times New Roman, Tahoma, or Comic Sans etc - any font you have installed in Windows 10.
Right in the notepad app, you can find and copy the desired font name. Open the menu item Format - Font... and browse for the desired font as shown below: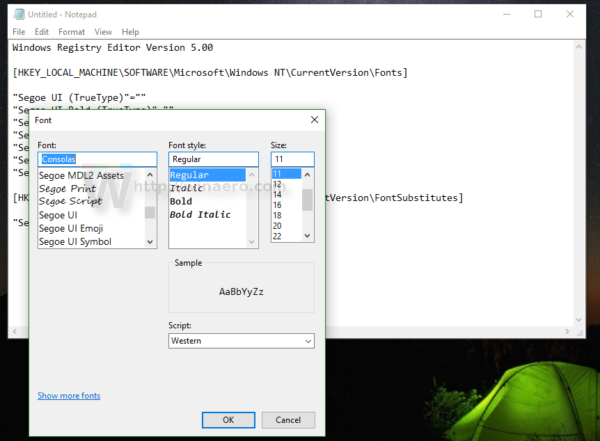
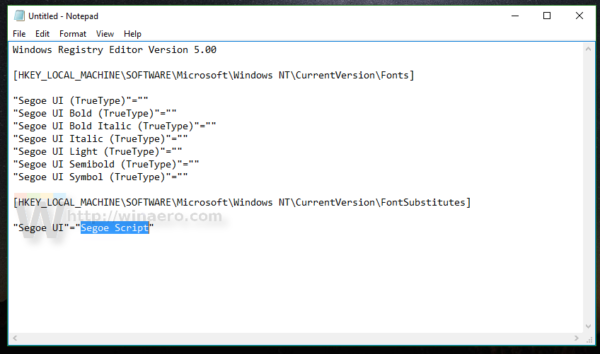
For example, let's set the system font to the fancy Segoe Script font. The text you paste in Notepad will look as follows:
Windows Registry Editor Version 5.00 [HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows NT\CurrentVersion\Fonts] "Segoe UI (TrueType)"="" "Segoe UI Bold (TrueType)"="" "Segoe UI Bold Italic (TrueType)"="" "Segoe UI Italic (TrueType)"="" "Segoe UI Light (TrueType)"="" "Segoe UI Semibold (TrueType)"="" "Segoe UI Symbol (TrueType)"="" [HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows NT\CurrentVersion\FontSubstitutes] "Segoe UI"="Segoe Script"
 Save the text you entered as a *.reg file. You can save it in any desired location with any name. Put the file name in quotes to add the *.reg extension to your file, otherwise Notepad will save it as a text file. See the following screenshot:
Save the text you entered as a *.reg file. You can save it in any desired location with any name. Put the file name in quotes to add the *.reg extension to your file, otherwise Notepad will save it as a text file. See the following screenshot: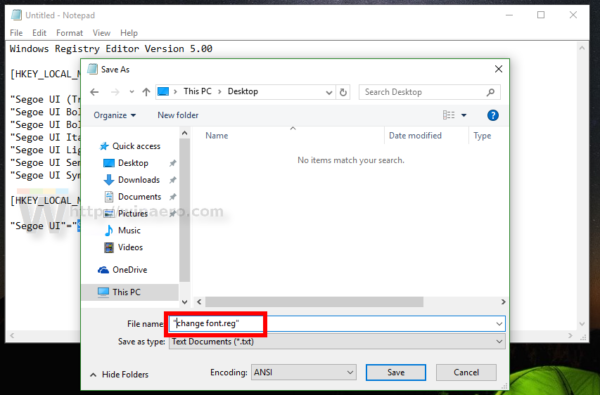
Now, double click the file you saved to apply the Registry tweak and change the font. Answer Yes to all requests:
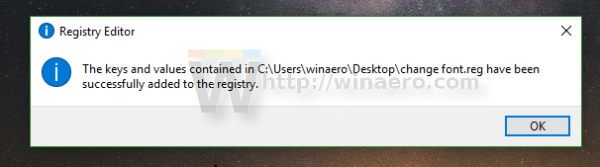 Now, sign out from your Windows account and sign in back to see the changes in action. In our case, the result will be as follows:
Now, sign out from your Windows account and sign in back to see the changes in action. In our case, the result will be as follows: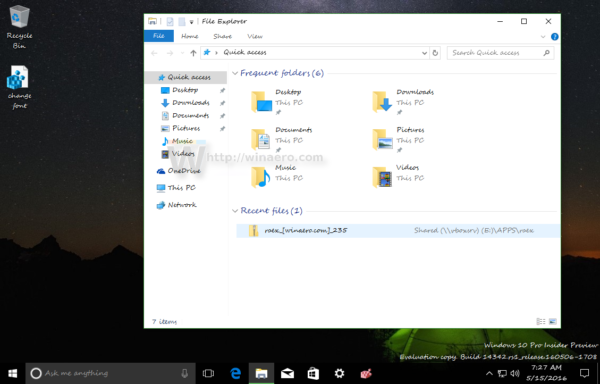
That's it.
To undo the tweak you applied, I prepared two ready-to-use Registry files. The first one is as described above and contains the font tweak. You can use it as a template that you can edit and substitute the desired font. The other one is "restore defaults.reg", which restores default fonts to Segoe UI. Once you merge these files, do not forget to sign out to apply the changes.
Support us
Winaero greatly relies on your support. You can help the site keep bringing you interesting and useful content and software by using these options:

You should defo add this to your tweaker if you didn’t already.
It is in TO DO already
Sergey, many thanks, all OK now…..Stan
I tried changing the default font to Segoe UI 7 (the original Segoe) but the time on my taskbar has a square instead of : and the title bar on paint.net window bars has the wrong font, can you fix this on 0.11.2.1? Thanks
I had the exact same problem in 0.12.1.0. I’ve checked all the fonts and they all contain the colon ( : ) character in the proper place. What would be the root of this problem?
I suppose that is because windows uses fancy symbols for that part of the taskbar from the Segoe UI font that are not in other fonts perhaps
how can i fix the ( : ) same problem. i have a square instead of the colon.
If you want the font called .VnTeknical Regular In The Control Panel but set the icons to large
Hi! I download the registry files “Download Replace the Segoe UI font with any other font” and just open, appeared the file “Start sound changer win8”! Probadly a little mistake :-P
Thanks! Fixing.
The link is fixed. I am sorry for this.
Hi,
Your download link for this registry file points to the wrong place. It’s downloading your Win 8 Start Sound tweak instead.
Fixed
Thx for this tweak, please provide the correct files for setting the default settings. When I click download I get a sound volume setting.
The link is fixed!
Wrong download files…:-(
I am sorry for this.
The link is fixed.
Hey Sergey, your tip sounds great, but using it messed the design of my system. So I want to get back to default settings. But your download link links not to the correct file. Please fix this. Thank you.
Tom
I am sorry for this.
The link is fixed.
False download file…:-(
Me too waiting for the right file :-)
I am sorry for this.
The link is fixed.
I am sorry for this.
The link is fixed.
Thank you!
Hi Sergey, I like to point out that although the tweak works, it has a drawback, you cannot use the Segoe UI in others applications because the tweak is global and not just only for the system.
E.g., after I have changed to Tahoma, my docs done with Segoe UI have changed to Tahoma, and in the dropdown fonts list, the Segoe UI is gone. I have used the tweak from your Winaero Tweaker.
Hi Sergei,
Thank you very much for a useful tweaker.
In Windows 10 I have a very small fonts, but not those that can be controlled using your WinaeroTweaker, or using Windows Control Panel \ All Control Panel Items \ Fonts \ Font settings, or by editing the registry branch HKEY_CURRENT_USER \ Control Panel \ Desktop \ WindowMetrics.
For example, most of the windows and panels in the Control Panel, buttons in the Action Center or the whole content of your WinaeroTweaker.
Who better than you is understanding how to change these fonts ))
Can you give me some useful advice?
The script works fine. Thanks you!
Windows 10Pro & Enterprise LTSB_n
I had an App : https://c1.staticflickr.com/9/8676/28762240872_6135c7bf1d_o.png . It used a customize font (VK Sans Serif) and installed to system font: https://c1.staticflickr.com/9/8765/28866943145_890b57850a_o.png . Even I used Winaero Tweaker to change font, I don’t see above font : https://c1.staticflickr.com/9/8773/28762240922_bba9f0f762_o.png . How do I fix ?
Hi!
I don’t think Windows 10 supports VGA resolution fonts for the status bar (which include fonts like Courier, FixedSys, System) which is unfortunate so it is probably not listing VGA resolution fonts which are old raster like fonts. I can see in the screenshot you provided that your font is a VGA resolution font (VGA Res) so I don’t think it can be shown sadly..
Hello! The fixes for the fonts did not work for me. It still stays the same.
Didn’t really work for me, I used the Winaero Tool to change all the fonts I could, works perfectly in the explorer windows, browser tabs etc, but unfortunately not for the start menu. I tried changing the system fonts in the registry (FontSubstitutes) and with your .reg-file, but both didn’t make any change.
Any ideas?
Hi there!
I might have a little problem: Since changing the system font, my on-screen keyboard seems to be bugged. Instead of numbers on the numpad I get some kind of boxes/squares, as if some characters are missing… Same goes for
some of the special characters like the dolar sign. I can write them down, though, it just makes me “blind”, as I can’t see some keys correctly… Can you please give me a hand? I already tried resetting the changes, but it didn’t worked, stoll getting the boxes…
Kind regards,
Michael
same to me. the numbers on the tablet keyboard are gone. same for the commands on the movie app. is there any way to restore them?
You must re-install Segoe UI Symbol on your PC to appear the icons again.
EDIT:
reading the article made me think a little bit,so i checked the registry and it came out that for a reason i do not know there were missing correspondences. some segoe fonts equalled to nothing. simply using the reset fonts REGISTRY FILE (not the option on the program) solved the issue.
Sergey, Thank you, all OK now…
I just downloaded the Winaero Tweaker and tried to change my small fonts which appeared after a minor glitch of my computer. As reported above, my fonts didn’t enlarge either. Suggestions?
Thank you so much
After changing the fonts using tweaker i cant login again in my windows 10…it hang up….please help
Safe mode?
!!!!! Urgent Help Needed !!!!!!
After running the suggested method. I lost all text display in window Explorer and the text in the window (button left). Help! How do I restore now without even seeing any text in Window Explorer.
Well, open winaero tweaker.
go to the system font option.
click on the “reset this page to defaults” on the toolbar.
restart the os.
this will resolve the issue.
Thanks for sharing the tweak.
just one thing i would like to said.
If you see tofu (a square) in some UWP app after applied this tweak,
you can try set the “Segoe UI Symbol (TrueType)”=”” back to default.
Guys, please help me after I did it, my lap is not working – means can’t put password and it can’t worked. Please, help me!!!
Try to re-installing Windows 10 on your laptop. Or try resetting via Advanced Boot Options (Windows 10 DVD required if your laptop has DVD tray disc) and then click Reset This PC. After that, follow the instructions on screen.
why do we not have an option to change the system font’s size?
Most definitely! I, too, wish I could change the SIZE of the System Font, but that isn’t possible with the current configuration of Winero Tweaker 0.12.0.0.
You can find sizes that possible to change under the “Advanced appearance” section. System font doesn’t support it.
Thank you for your reply. I see that the new Windows October release has a way to change system fonts, but my main problem is that I can’t change the very topmost headers. For instance, the very top line of a window, or the columns in the File Explorer (cut, paste, pin to quick access, etc.) I know that I can change this through resolution in Appearance, such as 125% or 150%, but that increases the whole screen and it’s all much too big. I tried changing the size of the system fonts with the new slider in this release, but it’s not affecting any of those aforementioned top headers. That may possibly be is that I’m hooked on Winero Tweaker and it’s overriding the Windows version of fonts??
Hi, I want to do the same — change the size of the system font, which is too small at the moment. Let me know please if you found a way. Thanks, sue.
Hi all,
I’m absolutely sure that I used to be able to change the system (menu) font size in recent versions of WinAero Tweaker. For years, I had been using Palatino 14pt. However, now it seems that I can’t find a way to change the font size anymore!?
Please help
PS:
I found it. It is actually not to be found under “fonts”, but under “menus”. There, font and size can be changed.
I change the size menu fonts. Everything is ok except Ms Office ribbon fonts are to big now. File, Design, Layout … are at least 2 times bigger than other Win 10 menu fonts. What should I do? Pls help.
thx
Quick question – I’m struggling to get the font size increased on my task bar and on some random menus– certain apps seem to be not impacted by tweaks (Steam for example). I’m more concerned about the taskbar for now, but I’d like to be able to make some universal changes. Any way to increase font size across everything (without making all other apps and icons huge too)?
Somehow search cant be used on windows 11 if I change the system font..
Is this works on Windows 11?
It works great, thank you for providing these tools for free!
Unfortunately, Inkscape (at least on Windows 11) seems to rely on Segoe UI being the system font. It becomes unusable due to wacky characters. Oh well, I can always change the system font quickly and easily using the Tweaker. Thanks again!
Why do some Fonts appear lower down to the point they are cut off…
At first i thought it was a visual bug within win aero but its not, In Certain areas of windows the text is cut off vertically because the font is around half way lower down than is should be
The font in question is Josefin Sans and here are some screenshots [Large Font size to make the bug obvious, actual system font is set to 9]: https://imgur.com/a/G6WjL0P
LOVE Win Areo! Windows 10 keeps changing the font settings from time to time though (I customize the Icon fonts and most others too). It’s been driving me mad for a long time. Is there a way to stop it from touching my settings? Anyway, I love your work and Windows would SUCK without it. Thank you!